Number Of Slots Per Pole
The number of slots per pole per phase determines how the winding layout is arranged. It is also disclosing information about the winding factor and its harmonics.
We can see that each phase’s pole is divided into two coils which are equal to two solts/pole/phase, Hence, when you are allowed to have 24 turns/phase you will have 24 turns divided into two poles which are 12 turns /pole and 6 turns/slot. If you would please share your FEMM model with us that would be great!
If the number of slots/pole/phase is an integer, the winding is called integer-slot winding.
If the number of slots/pole/phase is fractional and superior to 1, the winding is called fractional-slot winding.
- Pole Pitch is naturally equal to the total number of armature slots divided by the number of poles in the machine. If there are 96 slots on the armature periphery and 4 numbers of poles in the machine, the numbers of armature slots come between two adjacent poles centres would be 96/4 = 24. Hence, the pole pitch of that DC machine would be 24.
- Machines the number of slots per pole usually lies a) between 2 to 4 b) between 6 to 8 c) between 9 to 16 d) between 20 to 30.
If the number of slots/pole/phase is fractional and inferior to 1, the winding is called concentrated winding.
Windings with the same number of slots/pole/phase $q$ have the same winding factor. Their winding layouts consist of the same basic sequence repeated by the number of winding symmetries (or machine periodicity).
Example:
10-pole 12-slot single-layer 3-phase winding: $q=frac{12}{10cdot 3}=frac{2}{5}$, fundamental winding factor: 0.966, one winding symmetry.
20-pole 24-slot single-layer 3-phase winding: $q=frac{24}{20cdot 3}=frac{2}{5}$, fundamental winding factor: 0.966, two winding symmetries.
The number of slots/pole/phase is also an indicator about what winding factor and winding-factor harmnoics one can expect.
Example 1:
The harmonic spectrum of the winding factor of 4-pole 3-phase integer-slot windings in Fig. 1 shows that an increasing number of slots/pole/phase (from $q=1$ for the 12-slot winding to $q=5$ for the 60-slot winding) leads to a steady decrease of the fundamental winding factor. However, since the coils are distributed over several slots per pole per phase, the back-EMF gets more sinusoidal. This fact is reflected in significantly reduced winding factor harmonics of order three and higher, cf. Fig. 1.
Fig. 1 Winding factor harmonics for 4-pole 3-phase integer-slot windings with different number of slots/pole/phase.
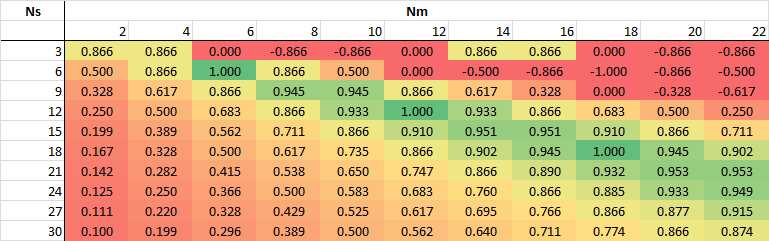
Example 2:
For concentrated windings, the fundamental winding factor increases and decreases as a function of the number of slots/pole/phase as shown in Fig. 2. The highest fundamental winding factors are found when the number of slots is closest to the number of poles, ie. $q0007pprox 1/3$.
Fig. 2 Fundamental winding factor for concentrated windings as a function of the number of slots/pole/phase [1].
References:
[1] Florence Meier, Permanent-Magnet Synchronous Machines with Non-Overlapping Concentrated Windings for Low-Speed Direct-Drive Applications, Phd Thesis, Royal Institute of Technology (KTH), July 2008
Read about another glossary term
Source
2011 International Conference on Electrical Machines and Systems>1 - 4
Abstract
Identifiers
| book ISBN : | 978-1-4577-1044-5 |
| book e-ISBN : | 978-1-4577-1043-8 , 978-1-4577-1042-1 |
| DOI | 10.1109/ICEMS.2011.6073738 |
Authors
User assignment
Assignment remove confirmation
You're going to remove this assignment. Are you sure?
Liu, Ting

- College of Electrical and Information Engineering, Hunan University, 410082, China
Fractional Number Of Slots Per Pole
Huang, Shoudao
- College of Electrical and Information Engineering, Hunan University, 410082, China
Number Of Slots Per Pole Per Phase
Deng, Qiuling
- College of Electrical and Information Engineering, Hunan University, 410082, China
Pu, Qingyun
- College of Electrical and Information Engineering, Hunan University, 410082, China
Keywords
TorquePermanent magnetsWind turbinesForgingSynchronous generatorsHarmonic analysis
TorquePermanent magnetsWind turbinesForgingSynchronous generatorsHarmonic analysis